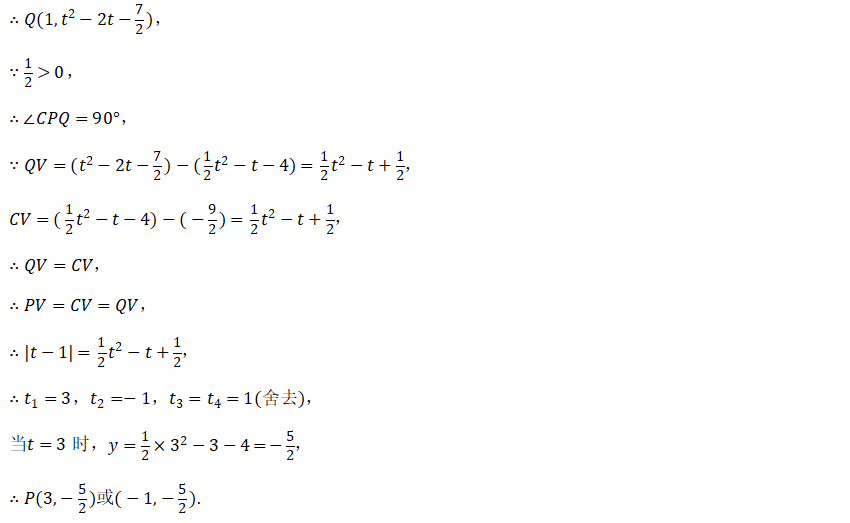2023常州中考数学题解与评价

2023常州中考数学题解与评价
LZH导览:
常州市2023年中考已经落下帷幕近两个月了,其中数学试题饱受争议,作为2023界常州中考的考生之一,我将从一下几个方面解答并评价这张试卷,并谈谈我个人对数学的看法,
- 试题概览
- 试题解答
- 试题评价
这也大概是我最后一次评价初中试卷啦~👏
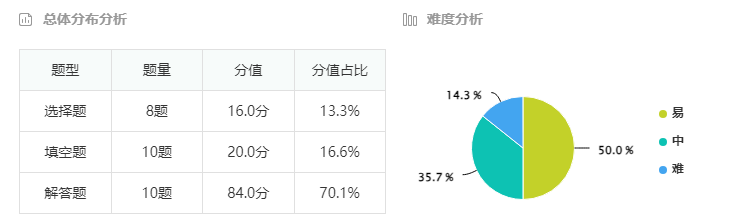
第一部分——试题概览


众所周知,常州中考数学试卷一共有28题,满分120分,选择填空都是2分一个,其中选择最后一道,填空最后一道和答题的后三道为压轴题(其中包含中档题15分左右,而真正压轴的分数大约为10分左右)
而要想得到较为满意的分数(115+),必须要保证前面的基础和中档部分一分不丢,并且还要留足大约半个小时进行检查,切不能和博主一样粗心大意,
本张试卷难度适中,但题目比较坑,想要得到高分有一定难度。
博主将试题分为$\color{gray}\text{简单}$、$\color{blue}\text{中档}$ 与 $\color{red}\text{困难}$ 3种难度
在下面的第二部分中,仅会讲解部分中档和所有的困难难度的题目。
第二部分——试题解答
1. 选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 答案 | $B$ | $B$ | $A$ | $A$ | $C$ | $C$ | $D$ | $D$ |
是不是很规律(bushi
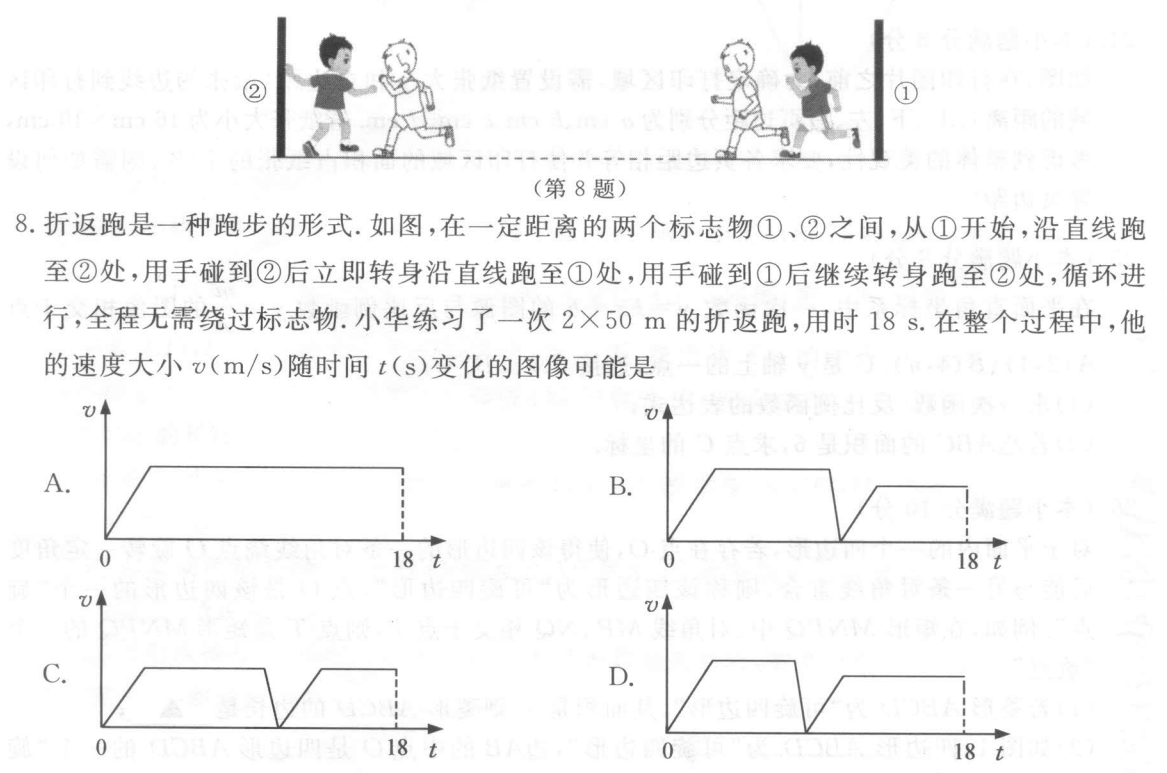
下面浅讲一下第8题:
考虑折返跑时两次距离相等,由于体力原因,在正常情况下,第二次折返后速度小于第一次时的速度,由于折返后与折返前的距离严格相等,且折返时速度为0,故折返返回起点所用时间严格大于从起点出发跑到折返点的时间。
这里也可以理解为:图像与坐标轴围成的两个梯形的面积严格相等
- 对于A选项 无折返,不合题意,排除
- 对于B选项 显然第二个梯形面积小于第一个梯形面积,不合题意,排除
- 对于C选项 同B选项的理由,排除
- 对于D选项 符合题意 故选D
试题难度:
2. 填空题
| 题号 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
|---|---|---|---|---|---|---|---|---|---|---|
| 答案 | ${3}$ | $y(x+2)(x-2)$ | $\dfrac{3}{2}$ | ${xy=10}$ | ${\pi a^3}$ | $\dfrac{5}{9}$ | $\dfrac{\sqrt{2}}{2}$ | ${4\sqrt{2}}$ | ${74}$ | $\dfrac{\sqrt{2}}{2}≤MP<\sqrt{5}$ |
其中第17题和18题讲一下:
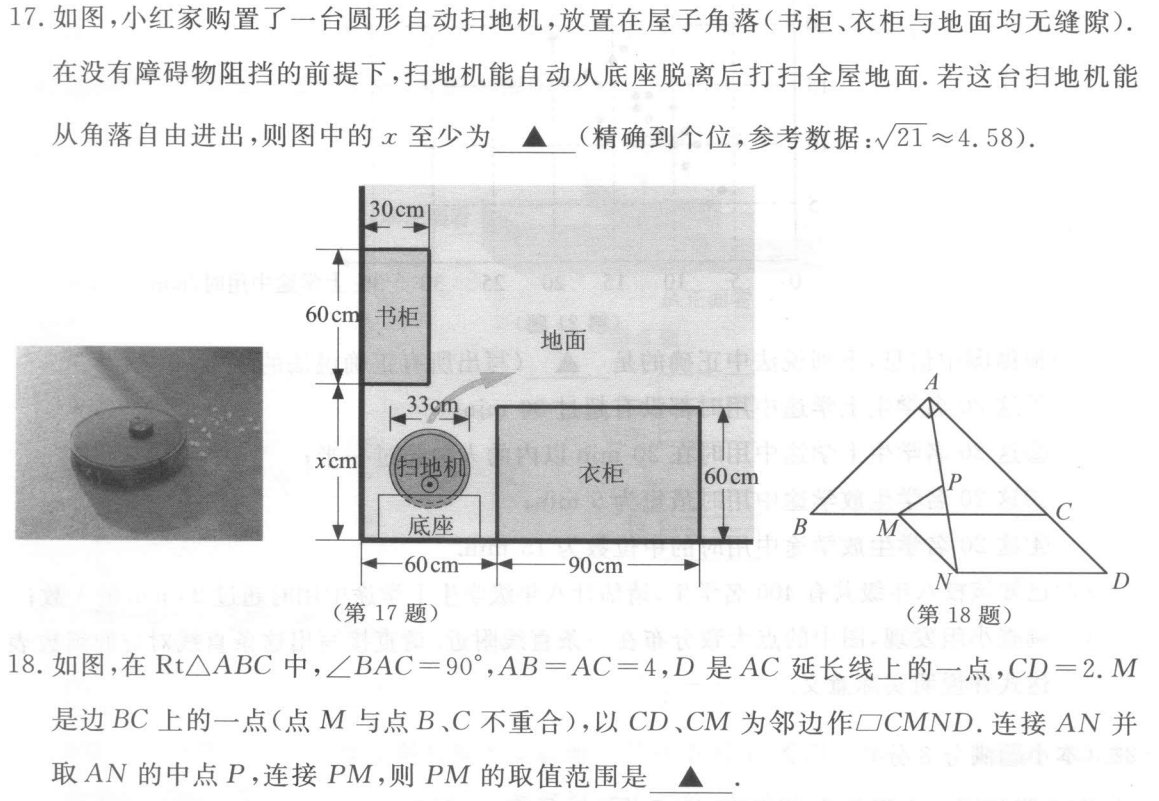
- 第17题解答:
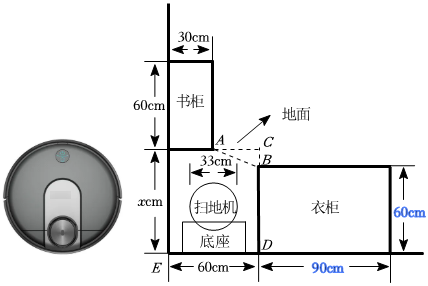
本题是看似复杂的送分题,考虑$AB$的长度至少为扫地机器人的半径,根据勾股定理即可得出答案
如图,连接$AB$,过点$A$作$AB//DE$交$DB$的延长线于点$C$,
则$AC=60-30=30(cm),BC=(x-60)cm.$
在$Rt△ABC$中,$BC=\sqrt{AB^2-AC^2}=\sqrt{33^2-30^2}=3\sqrt{21}\approx14$
于是有$x-60=14 \Rightarrow x=74$
所以答案为${74.}$
试题难度:
- 第18题解答:
有如下三种方法:
方法一:考虑P的运动轨迹(但不是很严谨)
$∵AB=AC=4,$
$∴AD=6,$
$∵△ABC$是等腰直角三角形,四边形$CNMD$是平行四边形,
$∴DN//BC,DN=BC,CD//MN,CD=MN,$
$∴∠ADN=∠ACB=45°=∠ABC=∠CMN,$
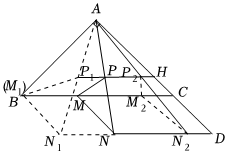
当$M$与$B$重合时,如图$P_2,M_2,N_2$,此时$MP$最长
$AN_1=\sqrt{4^2+2^2}=2\sqrt{5}$
$∵P_1$是中点,
$∴MP=\dfrac{1}{2}AN_1=\sqrt{5},$
当$MP⊥BC$时,如图$P_2,M_2,N_2,$此时$MP$最短
$∵P_1,P,P_2$是中点,
$∴P$的运动轨迹为平行于$BC$的线段,交$AC$于$H$,
$∴CH=3-2=1,$
$∵∠ACB=45°,$
$∴PH与BC$间的距离为$P_2M_2=\dfrac{\sqrt{2}}{2}CH=\dfrac{\sqrt{2}}{2},$
$∵M$不与$B$、$C$重合,
$∴\dfrac{\sqrt{2}}{2}≤MP<\sqrt{5}$
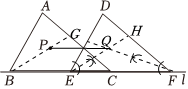
方法二:构造全等三角形(推荐)
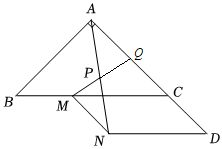
如图,延长$MP$交$AC$于点$Q$
由于$AP=PN$且$MN//AQ$
显然有 $△MPN≅△QPA(ASA)$
于是$AQ=MN=CD=2 \Rightarrow Q$为定点($AC$中点)
且恒有$MP=\dfrac{1}{2}MQ$
当$MQ$最大时,$MP$最大,此时$B$与$M$重合,
易得$MQ=2\sqrt{5}$,此时${MP}=\sqrt{5}$
当$MQ$最小时,$MP$最小,此时$QM⊥BC$,
易得$MQ=\sqrt{2}$,此时$MP=\dfrac{\sqrt{2}}{2}$
$∵M$不与$B$、$C$重合,
$∴\dfrac{\sqrt{2}}{2}≤MP<\sqrt{5}$
方法三:建系(下下策)
- 待填坑
试题难度:
3.解答题
19题解答
原式$=x^2+2x+1-2x-2=x^2-1,$
当$x=\sqrt{2}$时,原式$=2-1=1.$
试题难度:
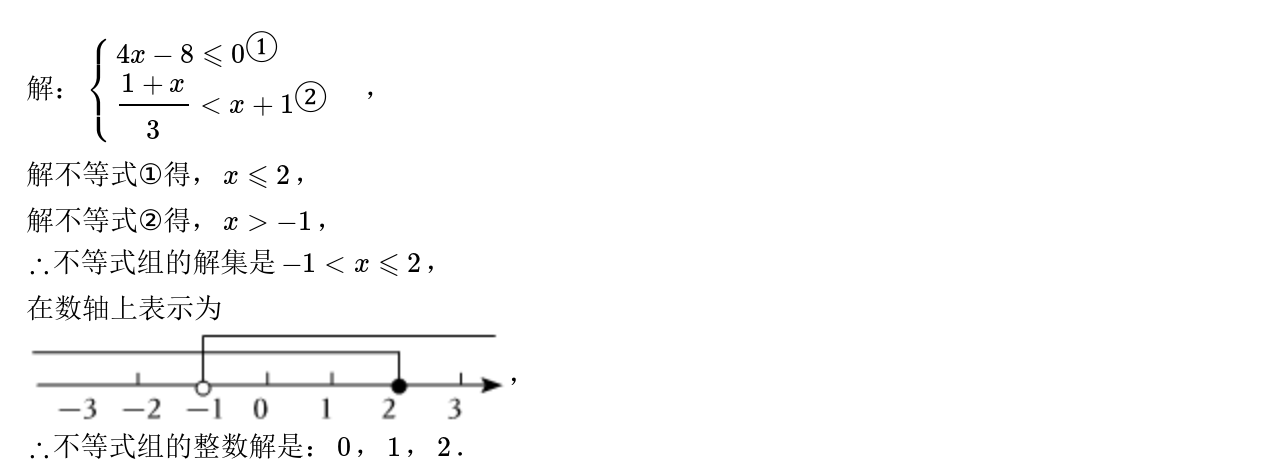
20题解答
试题难度:
$\color{red}\text{注意不要漏写整数解!!!}$
21题解答
(1) $②③$.
(2) 根据图中信息可知,上学途中用时超过${25min}$的学生有${1}$人,
故该校八年级学生上学途中用时超过${25min}$的人数为${400×120=20}$(人)
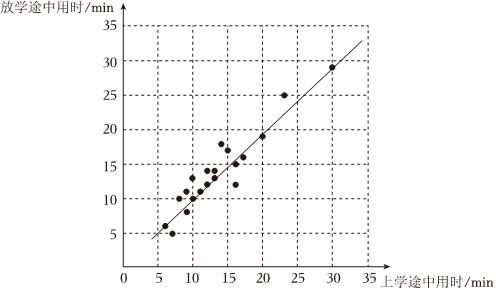
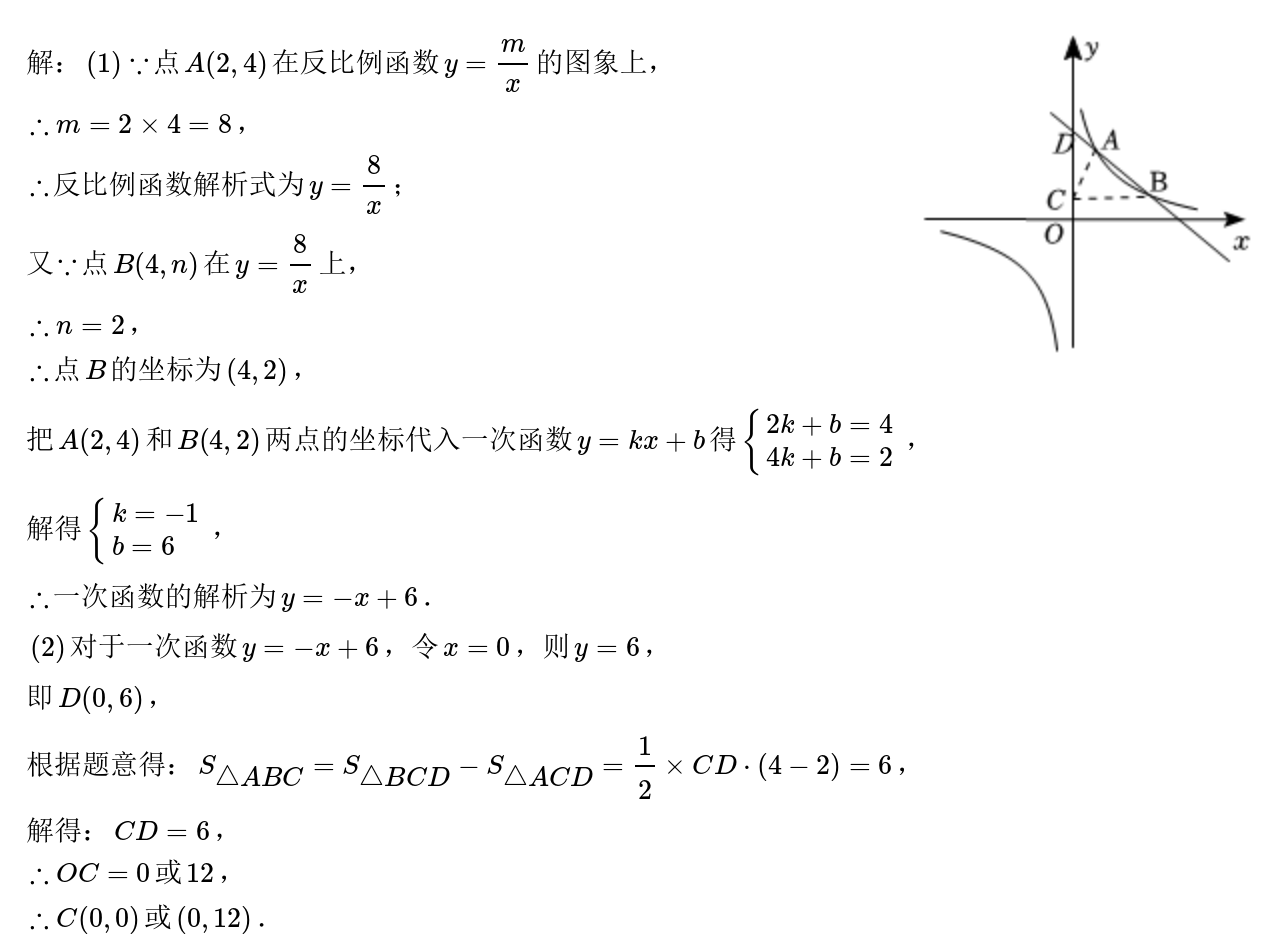
(3) 如图:
显然,直线的解析式为:$y=x$
实际意义:这条直线可近似反映该学校学生放学途中用时和上学途中用时的变化趋势,即:大多数同学上下学时间几乎相等
试题难度:
22题解答
(1) $\dfrac{2}{3}$
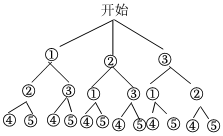
(2) 画树状图得:
共有12种等可能的结果,其中抽到的2个实数进行相应的运算后结果是无理数的有:①②⑤,①③④,①③⑤,②①⑤,②③④,②③⑤,③①④,③①⑤,③②④,③②⑤共10种,
$∴$抽到的2个实数进行相应的运算后结果是无理数的概率为$\dfrac{10}{12} = \dfrac{5}{6} $
答:抽到的2个实数进行相应的运算后结果是无理数的概率为$\dfrac{5}{6} $.
试题难度:
23题解答
(1) 证明:
${∵BE=CF}$,
${∴BE+EC=CF+EC}$,
${∴BC=EF}$,
在${△ABC}$和${△DEF}$中,
$AB=DE \ BC=EF \ AC=DF$
${∴△ABC≌△DEF(SSS)}$;
(2) ①如图,点${Q}$即为所求;
②PQ与BE的关系是:${PQ//BE}$且${PQ=BE}$
注意:关系分为数量关系与位置关系
试题难度:
24题解答
解:设页边距为${x cm}$,
根据题意得:$(16-2x)(10-2x)=16×10×70$%,
解得$x=1$或$x=12$(大于${10}$,舍去),
答:设置页边距为${1cm}$.
试题难度:
25题解答
$\color{red}\text{注意分类!}$
试题难度:
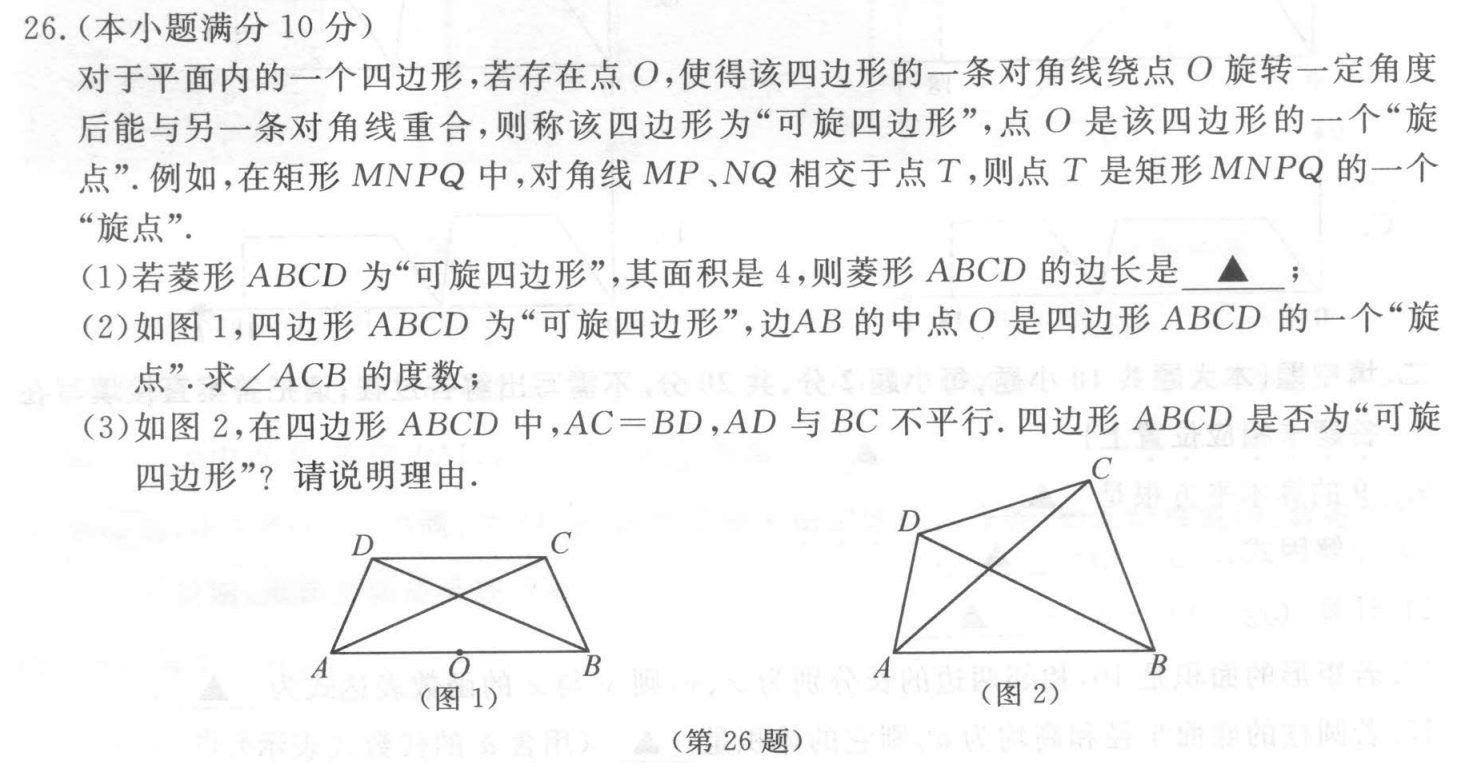
26题解答
我们首先对“可旋四边形”这个条件进行分析:
对于两条相交线段,如果他们的长度相等,通过分别做这两条线段的中垂线并找到他们的焦点,让一条直线绕着这个点旋转必然可以与另一条直线重合,故满足题意。
所以说:如果一个凸四边形满足对角线相等,那么这个四边形一定是“可旋四边形”。
下面考虑题中设问:
(1) 显然对角线相等的菱形是正方形,故答案为${2}$.
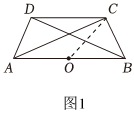
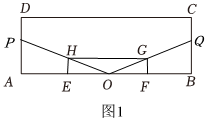
(2) 如图1:
连接$OC$,
$∵$四边形$ABCD$是“可旋四边形”,$O$为旋点,
$∴OC=OB$,
$∴∠OCB=∠OBC$,
$∵OA=OB$,
$∴OA=OC$,
$∴∠OAC=∠OCA$,
$∵∠OAC+∠OCA+∠OBC+∠OCB=180°$,
$∴2(∠OCA+∠OCB)=180°$,
$∴∠ACB=90°$;
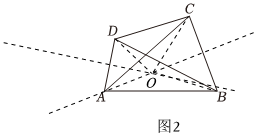
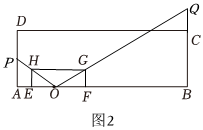
(3) 如图2:
四边形$ABCD$是“可旋四边形”,理由如下:
分别作$AD$和$BC$的垂直平分线,交于点$O$,连接$OA$,$OD$,$OB$,$OC$,
$∴OA=OD$,$OC=OB$,
$∵AC=BD$,
$∴△AOC≌△DOB(SSS)$,
$∴∠AOC=∠BOD$,
$∴∠AOD=∠BOC$,
$∴$四边形$ABCD$是“可旋四边形“.
试题难度:
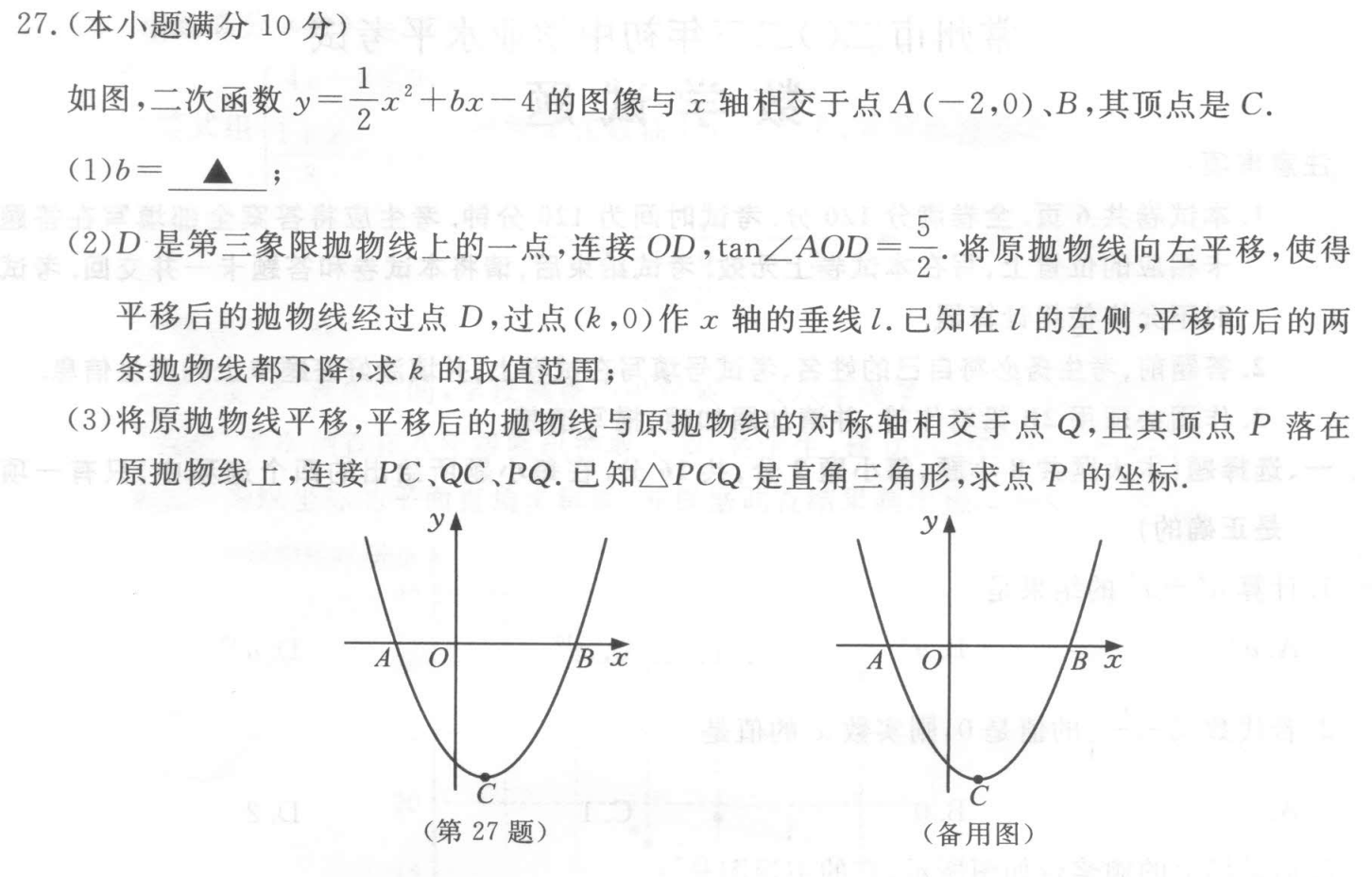
27题解答
(1) $b=-1$
(2)$∵tan∠AOD=\dfrac{5}{2}$,
$∴$设$D(2t,5t)$,
$\dfrac{1}{2} ×(2t)^2-2t-4=5t \Rightarrow t_1=-\dfrac{1}{2},t_2=4$(舍去)
$∴D(-1,-\dfrac{5}{2})$
$∵y=\dfrac{1}{2}x^2-x-4=\dfrac{1}{2}{(x-1)^2-\dfrac{9}{2}}$
$∴$新抛物线设为:$y=\dfrac{1}{2}{(x-m)^2-\dfrac{9}{2}}$
$-\dfrac{5}{2}=\dfrac{1}{2}{(m+1)^2-\dfrac{9}{2}}$
$∴m_1=-3,m_2=1$(舍去),
$∴y=\dfrac{1}{2}{(x+3)^2-\dfrac{9}{2}}$
$∵$在$l$的左侧,平移前后的两条抛物线都下降,
$∴k≤-3$;
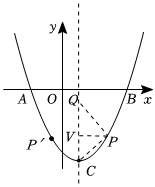
(3)如图,作$PV⊥CQ$于$V$
注意:本题的难点是一定要设顶点坐标式简化计算,否则后续解方程会出问题
设$P(t,\dfrac{1}{2}t^2-t-4)$
$∴$平移后的抛物线为:$y=\dfrac{1}{2}{(x-t)^2}+(\dfrac{1}{2}t^2-t-4)$
当$x=1$时,$y=t^2-2t-\dfrac{7}{2}$
好的下面就是没什么的技术含量的相似和计算了,看图吧:
试题难度:
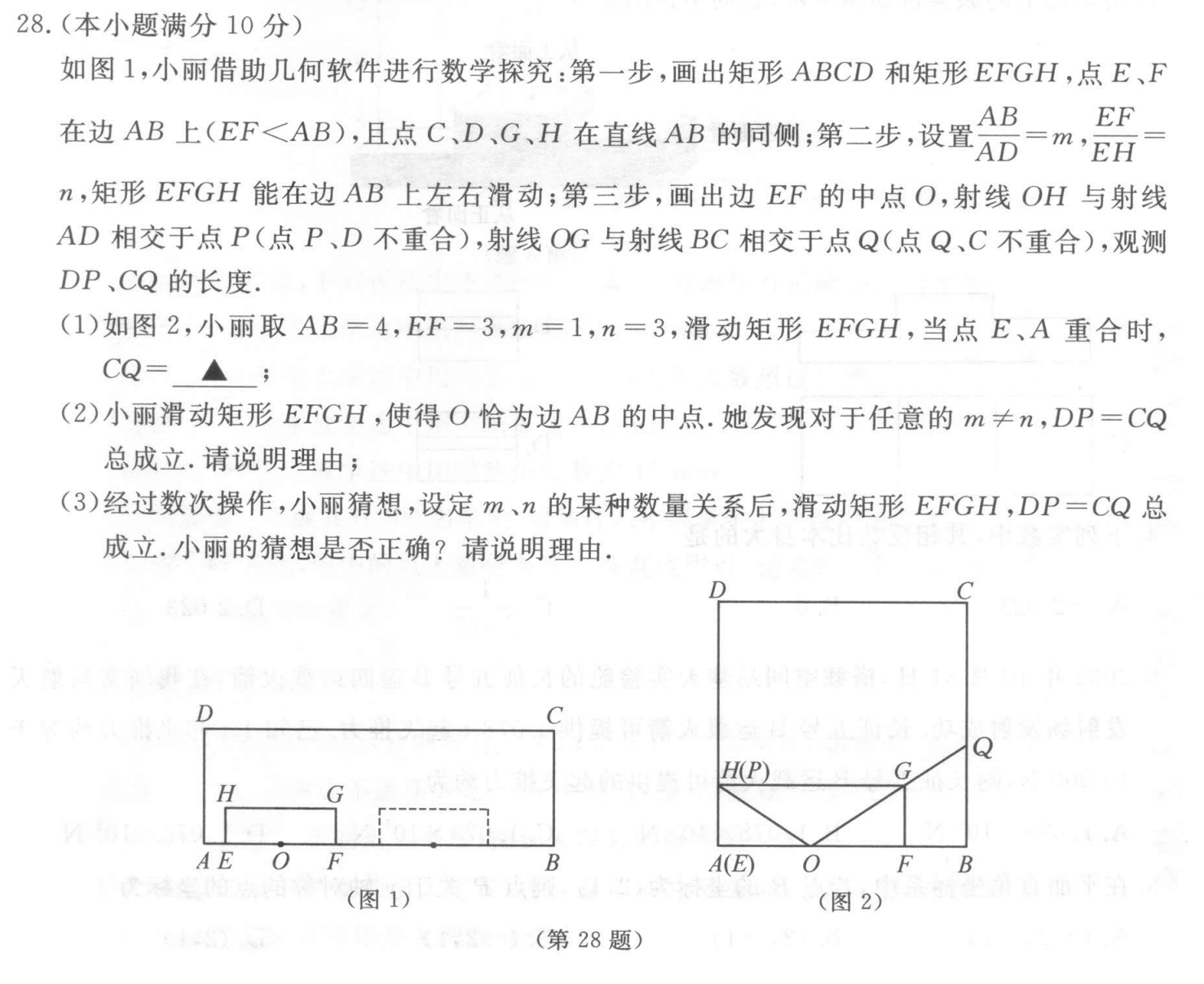
28题解答
试题难度:
第三部分——试题评价
试卷难度适中,某些方面来说比较灵活和新,但是依然考察十分基本的模型和思维方法,部分题目有陷阱,考察细致细心。总的来说,试卷质量还是比较高的,初三的同学可以拿来练手。